External Grid¶

Note

Power values of external grids are given in the generator system, therefore p_mw is negative if the external grid is absorbing power and positive if it is supplying/generating power.

Create Function¶

pandapower.create_ext_grid(net, bus, vm_pu=1.0, va_degree=0.0, name=None, in_service=True, s_sc_max_mva=nan, s_sc_min_mva=nan, rx_max=nan, rx_min=nan, max_p_mw=nan, min_p_mw=nan, max_q_mvar=nan, min_q_mvar=nan, index=None, r0x0_max=nan, x0x_max=nan, **kwargs)¶

Creates an external grid connection.

External grids represent the higher level power grid connection and are modelled as the slack bus in the power flow calculation.

INPUT:

net - pandapower network

bus (int) - bus where the slack is connected

OPTIONAL:

vm_pu (float, default 1.0) - voltage at the slack node in per unit

va_degree (float, default 0.) - voltage angle at the slack node in degrees*

name (string, default None) - name of of the external grid

in_service (boolean) - True for in_service or False for out of service

s_sc_max_mva (float, NaN) - maximal short circuit apparent power to calculate internal impedance of ext_grid for short circuit calculations

s_sc_min_mva (float, NaN) - minimal short circuit apparent power to calculate internal impedance of ext_grid for short circuit calculations

rx_max (float, NaN) - maximal R/X-ratio to calculate internal impedance of ext_grid for short circuit calculations

rx_min (float, NaN) - minimal R/X-ratio to calculate internal impedance of ext_grid for short circuit calculations

max_p_mw (float, NaN) - Maximum active power injection. Only respected for OPF

min_p_mw (float, NaN) - Minimum active power injection. Only respected for OPF

max_q_mvar (float, NaN) - Maximum reactive power injection. Only respected for OPF

min_q_mvar (float, NaN) - Minimum reactive power injection. Only respected for OPF

r0x0_max (float, NaN) - maximal R/X-ratio to calculate Zero sequence internal impedance of ext_grid

x0x_max (float, NaN) - maximal X0/X-ratio to calculate Zero sequence internal impedance of ext_grid

** only considered in loadflow if calculate_voltage_angles = True

EXAMPLE:

create_ext_grid(net, 1, voltage = 1.03)

For three phase load flow

create_ext_grid(net, 1, voltage = 1.03,s_sc_max_mva= 1000, rx_max=0.1,r0x0_max=0.1,x0x_max= 1.0 )

Input Parameters¶

net.ext_grid

Parameter	Datatype	Value Range	Explanation
name	string		name of the external grid
bus*	integer		index of connected bus
vm_pu*	float	\(>\) 0	voltage set point [p.u]
va_degree*	float		angle set point [degree]
max_p_mw**	float		Maximum active power
min_p_mw**	float		Minimum active power
max_q_mvar**	float		Maximum reactive power
min_q_mvar**	float		Minimum reactive power
s_sc_max_mva***	float	\(>\) 0	maximum short circuit power provision [MVA]
s_sc_min_mva***	float	\(>\) 0	minimum short circuit power provision [MVA]
rx_max***	float	0…1	maxium R/X ratio of short-circuit impedance
rx_min***	float	0…1	minimum R/X ratio of short-circuit impedance
r0x0_max****	float	0…1	maximal R/X-ratio to calculate Zero sequence internal impedance of ext_grid
x0x_max****	float	0…1	maximal X0/X-ratio to calculate Zero sequence internal impedance of ext_grid
in_service*	boolean	True / False	specifies if the external grid is in service.

*necessary for executing a power flow calculation
**optimal power flow parameter
***short-circuit calculation parameter
****Single phase short circuit/Three Phase load flow calculation parameters

Electric Model¶

** Balanced Load Flow** The external grid is modelled as a voltage source in the power flow calculation, which means the node the grid is connected to is treated as a slack node:

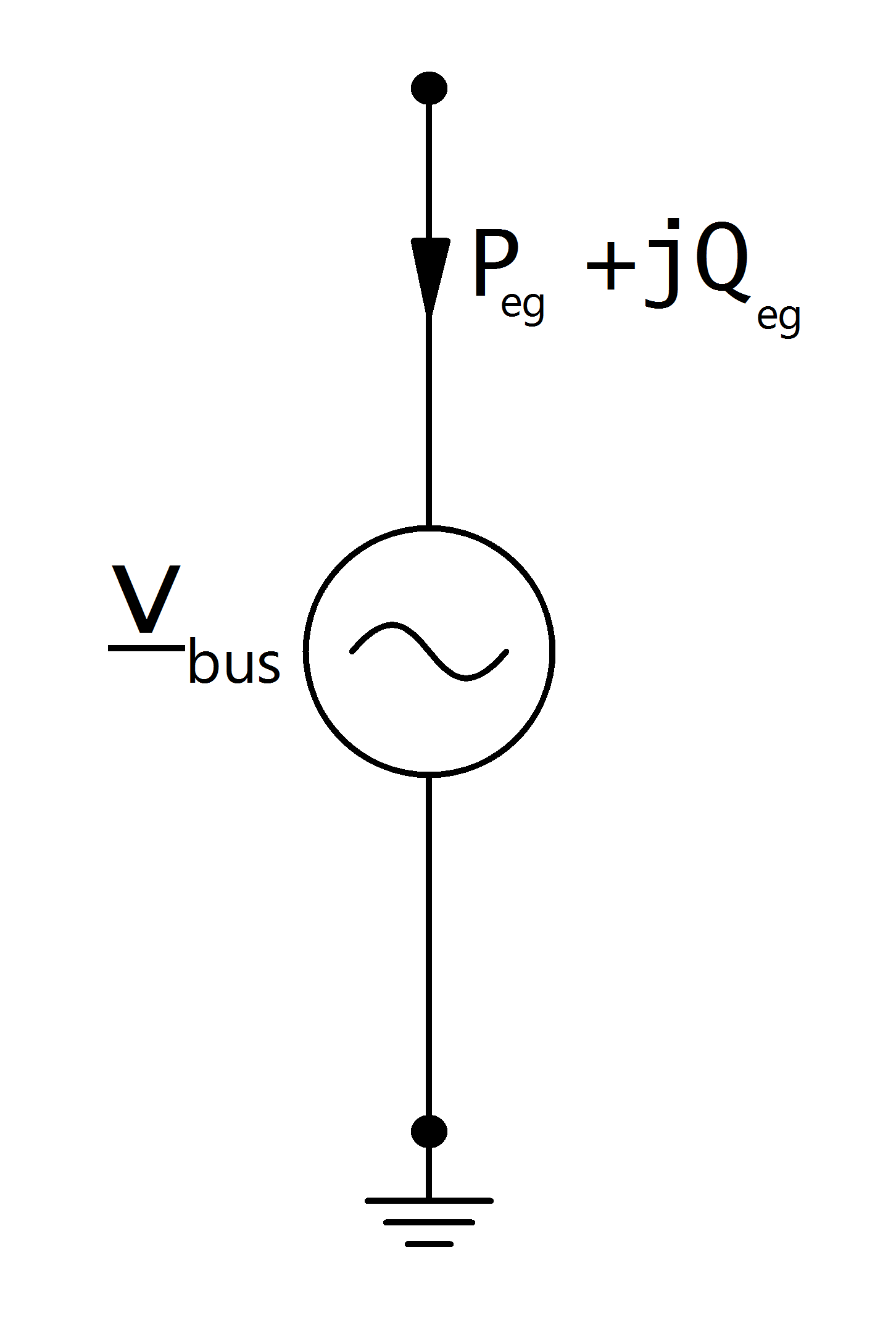
with:

\begin{align*} \underline{v}_{bus} &= vm\_pu \cdot e^{j \cdot \theta} \\ \theta &= shift\_degree \cdot \frac{\pi}{180} \end{align*}

** Unbalanced Load Flow / Single phase short ciruit **

The external grid is modelled as a voltage source for positive sequence model, which means the node the grid is connected to is treated as a slack node. For zero sequence and negative sequence external grid impedance is calculated:

\begin{align*} \underline{v}_{1} &= vm\_pu \cdot e^{j \cdot \theta} \\ \theta &= shift\_degree \cdot \frac{\pi}{180} \end{align*} \begin{align*} \underline{Z}_{0} &= c \cdot \frac{(vm \cdot e^{j \cdot \theta})^2}{S_{sc_mva}} \\ \theta &= shift\_degree \cdot \frac{\pi}{180} \end{align*} \begin{align*} \underline{v}_{bus} &= vm\_pu \cdot e^{j \cdot \theta} \\ \theta &= shift\_degree \cdot \frac{\pi}{180} \end{align*}

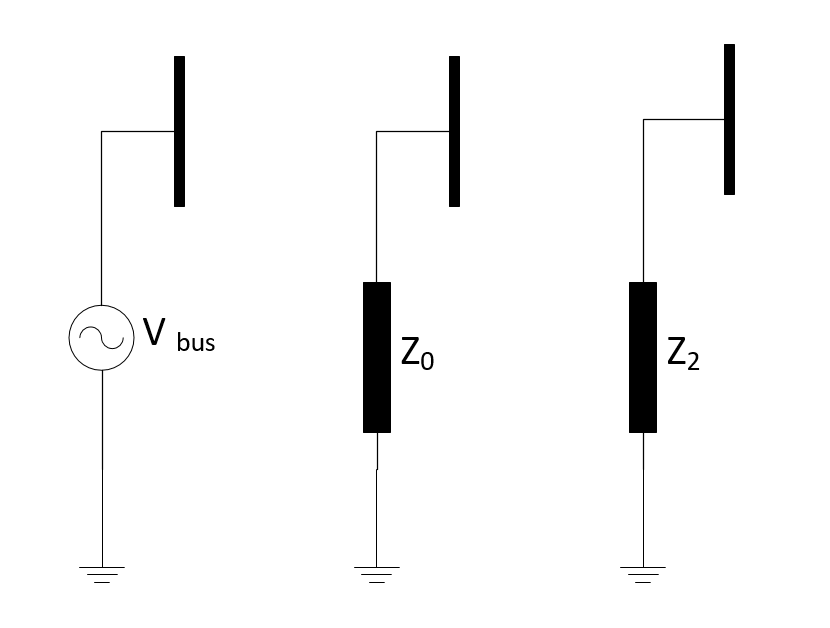
Result Parameters¶

net.res_ext_grid

Parameter	Datatype	Explanation
p_mw	float	active power supply at the external grid [MW]
q_mvar	float	reactive power supply at the external grid [MVar]

Active and reactive power feed-in / consumption at the slack node is a result of the power flow:

\begin{align*} p\_mw &= P_{eg} \\ q\_mvar &= Q_{eg} \end{align*}

net.res_ext_grid_3ph

Parameter	Datatype	Explanation
p_a_mw	float	active power supply at the external grid : Phase A [MW]
q_a_mvar	float	reactive power supply at the external grid : Phase A [MVar]
p_b_mw	float	active power supply at the external grid : Phase B [MW]
q_b_mvar	float	reactive power supply at the external grid : Phase B [MVar]
p_c_mw	float	active power supply at the external grid : Phase C [MW]
q_c_mvar	float	reactive power supply at the external grid : Phase C [MVar]

Active and reactive power feed-in / consumption at the slack node is a result of the power flow:

\begin{align*} p\_mw_{phase} &= P_{eg_{phase}} \\ q\_mvar_{phase} &= Q_{eg_{phase}} \end{align*}