Asymmetric Load¶

Note

Loads should always have a positive p_mw value, since all power values are given in the consumer system. If you want to model constant generation, use a Static Generator (sgen element) instead of a negative load. With Asymmetric Load three phase load values can be supplied seperately

Create Function¶

pandapower.create_asymmetric_load(net, bus, p_a_mw=0, p_b_mw=0, p_c_mw=0, q_a_mvar=0, q_b_mvar=0, q_c_mvar=0, sn_mva=nan, name=None, scaling=1.0, index=None, in_service=True, type='wye')¶

Adds one 3 phase load in table net[“asymmetric_load”].

All loads are modelled in the consumer system, meaning load is positive and generation is negative active power. Please pay attention to the correct signing of the reactive power as well.

INPUT:

net - The net within this load should be created

bus (int) - The bus id to which the load is connected

OPTIONAL:

p_a_mw (float, default 0) - The real power for Phase A load

p_b_mw (float, default 0) - The real power for Phase B load

p_c_mw (float, default 0) - The real power for Phase C load

postive value -> load
negative value -> generation

q_a_mvar float, default 0) - The reactive power for Phase A load

q_b_mvar float, default 0) - The reactive power for Phase B load

q_c_mvar (float, default 0) - The reactive power for Phase C load

sn_kva (float, default: None) - Nominal power of the load

name (string, default: None) - The name for this load

scaling (float, default: 1.) - An OPTIONAL scaling factor to be set customly

type (string,default: wye) - type variable to classify three ph load: delta/wye

index (int,default: None) - Force a specified ID if it is available. If None, the index one higher than the highest already existing index is selected.

in_service (boolean) - True for in_service or False for out of service

OUTPUT:

index (int) - The unique ID of the created element

EXAMPLE:

create_asymmetric_load(net, bus=0, p_c_mw = 9., q_c_mvar = 1.8)

Creates a single phase wye type load

Input Parameters¶

net.asymmetric_load

Parameter	Datatype	Value Range	Explanation
name	string		name of the load
bus *	integer		index of connected bus
p_a_mw*	float	\(\geq 0\)	Phase A active power of the load [MW]
p_b_mw*	float	\(\geq 0\)	Phase B active power of the load [MW]
p_c_mw*	float	\(\geq 0\)	Phase C active power of the load [MW]
q_a_mvar*	float		Phase A reactive power of the load [MVar]
q_b_mvar*	float		Phase B reactive power of the load [MVar]
q_c_mvar*	float		Phase C reactive power of the load [MVar]
const_z_percent*	float	\([0,100]\)	percentage of p_mw and q_mvar that is associated to constant impedance load at rated voltage [\(\%\)]
const_i_percent*	float	\([0,100]\)	percentage of p_mw and q_mvar that is associated to constant current load at rated voltage [\(\%\)]
sn_mva	float	\(>0\)	rated power of the load [kVA]
scaling *	float	\(\geq 0\)	scaling factor for active and reactive power
in_service*	boolean	True / False	specifies if the load is in service.
type*	String	wye/delta	Connection Type of 3 Phase Load(Valid for three phase load flow only)
controllable**	bool		States if load is controllable or not, load will not be used as a flexibilty if it is not controllable
max_p_mw**	float		Maximum active power
min_p_mw**	float		Minimum active power
max_q_mvar**	float		Maximum reactive power
min_q_mvar**	float		Minimum reactive power

*necessary for executing a power flow calculation.

Note

The apparent power value sn_mva is provided as additional information for usage in controller or other applications based on panadapower. It is not considered in the power flow!
‘wye’ is the same as PH-E loads
For ‘delta’ loads line-earth voltages and powers are converted to line-line values

Electric Model¶

Loads are modelled as PQ-buses in the power flow calculation.

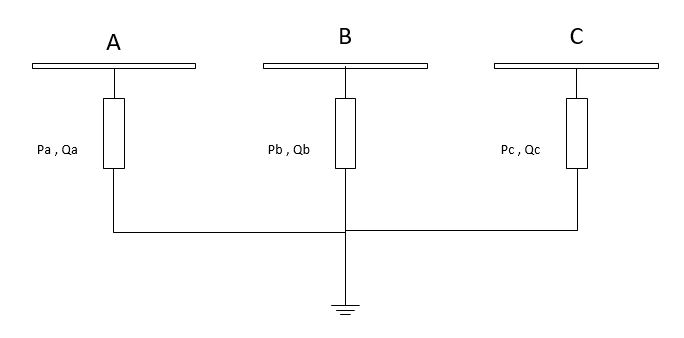
Wye Load

Delta Load

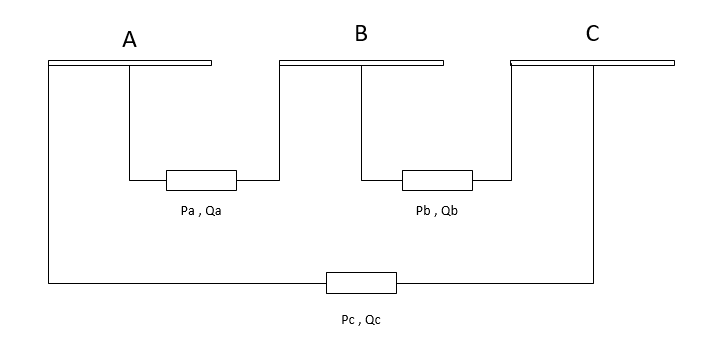
Even though power values are entered as Line-ground \(P_{a},Q_{a}\), for delta loads, Power values are actually line-line powers i.e. \(P_{ab},Q_{ab}\)

So, in the algorithm :

Line-ground voltages \(V_{a}\) are converted to line-line voltages \(V_{ab}\). Line-Line currents are then converted to Line-ground currents \(I_{a}\).

\(I_{a}= T. \frac{S_{ab}}{(V_{an}-V_{bn})}\)

\(I_{b}= T. \frac{S_{bc}}{(V_{bn}-V_{cn})}\)

\(I_{c}= T. \frac{S_{ca}}{(V_{cn}-V_{an})}\)

Where

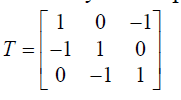
Result Parameters¶

net.res_asymmetric_load

Parameter	Datatype	Explanation
p_a_mw	float	resulting Phase A active power demand after scaling and after considering voltage dependence [MW]
q_a_mvar	float	resulting Phase A reactive power demand after scaling and after considering voltage dependence [MVar]
p_b_mw	float	resulting Phase B active power demand after scaling and after considering voltage dependence [MW]
q_b_mvar	float	resulting Phase B reactive power demand after scaling and after considering voltage dependence [MVar]
p_c_mw	float	resulting Phase C active power demand after scaling and after considering voltage dependence [MW]
q_c_mvar	float	resulting Phase C reactive power demand after scaling and after considering voltage dependence [MVar]