Line

See also

Unit Systems and Conventions
Standard Type Libraries

Create Function

Lines can be either created from the standard type library (create_line) or with custom values (create_line_from_parameters).

Note

Lines for 3 phase load flow uses zero sequence parameters which can be provided through a custom standard type using pandapower.create_std_type() and pandapower.add_zero_impedance_parameters()

Zero sequence parameters (Added through std_type For Three phase load flow) :

-r0_ohm_per_km (float) - zero sequence line resistance in ohm per km

-x0_ohm_per_km (float) - zero sequence line reactance in ohm per km

-c0_nf_per_km (float) - zero sequence line capacitance in nano Farad per km

pandapower.create_line(net, from_bus, to_bus, length_km, std_type, name=None, index=None, geodata=None, df=1.0, parallel=1, in_service=True, max_loading_percent=nan, alpha=nan, temperature_degree_celsius=nan, **kwargs)

Creates a line element in net[“line”] The line parameters are defined through the standard type library.

INPUT:

net - The net within this line should be created

from_bus (int) - ID of the bus on one side which the line will be connected with

to_bus (int) - ID of the bus on the other side which the line will be connected with

length_km (float) - The line length in km

std_type (string) - Name of a standard linetype :

• Pre-defined in standard_linetypes

or

• Customized std_type made using create_std_type()

OPTIONAL:

name (string, None) - A custom name for this line

index (int, None) - Force a specified ID if it is available. If None, the index one higher than the highest already existing index is selected.

geodata (Iterable[Tuple[int, int]|Tuple[float, float]], default None) - The geodata of the line. The first element should be the coordinates of from_bus and the last should be the coordinates of to_bus. The points in the middle represent the bending points of the line

in_service (boolean, True) - True for in_service or False for out of service

df (float, 1) - derating factor: maximal current of line in relation to nominal current of line (from 0 to 1)

parallel (integer, 1) - number of parallel line systems

max_loading_percent (float) - maximum current loading (only needed for OPF)

alpha (float) - temperature coefficient of resistance: R(T) = R(T_0) * (1 + alpha * (T - T_0)))

temperature_degree_celsius (float) - line temperature for which line resistance is adjusted

tdpf (bool) - whether the line is considered in the TDPF calculation

wind_speed_m_per_s (float) - wind speed at the line in m/s (TDPF)

wind_angle_degree (float) - angle of attack between the wind direction and the line (TDPF)

conductor_outer_diameter_m (float) - outer diameter of the line conductor in m (TDPF)

air_temperature_degree_celsius (float) - ambient temperature in °C (TDPF)

reference_temperature_degree_celsius (float) - reference temperature in °C for which r_ohm_per_km for the line is specified (TDPF)

solar_radiation_w_per_sq_m (float) - solar radiation on horizontal plane in W/m² (TDPF)

solar_absorptivity (float) - Albedo factor for absorptivity of the lines (TDPF)

emissivity (float) - Albedo factor for emissivity of the lines (TDPF)

r_theta_kelvin_per_mw (float) - thermal resistance of the line (TDPF, only for simplified method)

mc_joule_per_m_k (float) - specific mass of the conductor multiplied by the specific thermal capacity of the material (TDPF, only for thermal inertia consideration with tdpf_delay_s parameter)

OUTPUT:

index (int) - The unique ID of the created line

EXAMPLE:

create_line(net, from_bus = 0, to_bus = 1, length_km=0.1, std_type=”NAYY 4x50 SE”, name = “line1”)

pandapower.create_line_from_parameters(net, from_bus, to_bus, length_km, r_ohm_per_km, x_ohm_per_km, c_nf_per_km, max_i_ka, name=None, index=None, type=None, geodata=None, in_service=True, df=1.0, parallel=1, g_us_per_km=0.0, max_loading_percent=nan, alpha=nan, temperature_degree_celsius=nan, r0_ohm_per_km=nan, x0_ohm_per_km=nan, c0_nf_per_km=nan, g0_us_per_km=0, endtemp_degree=nan, **kwargs)

Creates a line element in net[“line”] from line parameters.

INPUT:

net - The net within this line should be created

from_bus (int) - ID of the bus on one side which the line will be connected with

to_bus (int) - ID of the bus on the other side which the line will be connected with

length_km (float) - The line length in km

r_ohm_per_km (float) - line resistance in ohm per km

x_ohm_per_km (float) - line reactance in ohm per km

c_nf_per_km (float) - line capacitance (line-to-earth) in nano Farad per km

r0_ohm_per_km (float) - zero sequence line resistance in ohm per km

x0_ohm_per_km (float) - zero sequence line reactance in ohm per km

c0_nf_per_km (float) - zero sequence line capacitance in nano Farad per km

max_i_ka (float) - maximum thermal current in kilo Ampere

OPTIONAL:

name (string, None) - A custom name for this line

index (int, None) - Force a specified ID if it is available. If None, the index one higher than the highest already existing index is selected.

in_service (boolean, True) - True for in_service or False for out of service

type (str, None) - type of line (“ol” for overhead line or “cs” for cable system)

df (float, 1) - derating factor: maximal current of line in relation to nominal current of line (from 0 to 1)

g_us_per_km (float, 0) - dielectric conductance in micro Siemens per km

g0_us_per_km (float, 0) - zero sequence dielectric conductance in micro Siemens per km

parallel (integer, 1) - number of parallel line systems

geodata (array, default None, shape= (,2)) - The geodata of the line. The first row should be the coordinates of bus a and the last should be the coordinates of bus b. The points in the middle represent the bending points of the line

max_loading_percent (float) - maximum current loading (only needed for OPF)

alpha (float) - temperature coefficient of resistance: R(T) = R(T_0) * (1 + alpha * (T - T_0)))

temperature_degree_celsius (float) - line temperature for which line resistance is adjusted

tdpf (bool) - whether the line is considered in the TDPF calculation

wind_speed_m_per_s (float) - wind speed at the line in m/s (TDPF)

wind_angle_degree (float) - angle of attack between the wind direction and the line (TDPF)

conductor_outer_diameter_m (float) - outer diameter of the line conductor in m (TDPF)

air_temperature_degree_celsius (float) - ambient temperature in °C (TDPF)

reference_temperature_degree_celsius (float) - reference temperature in °C for which r_ohm_per_km for the line is specified (TDPF)

solar_radiation_w_per_sq_m (float) - solar radiation on horizontal plane in W/m² (TDPF)

solar_absorptivity (float) - Albedo factor for absorptivity of the lines (TDPF)

emissivity (float) - Albedo factor for emissivity of the lines (TDPF)

r_theta_kelvin_per_mw (float) - thermal resistance of the line (TDPF, only for simplified method)

mc_joule_per_m_k (float) - specific mass of the conductor multiplied by the specific thermal capacity of the material (TDPF, only for thermal inertia consideration with tdpf_delay_s parameter)

OUTPUT:

index (int) - The unique ID of the created line

EXAMPLE:

create_line_from_parameters(net, from_bus = 0, to_bus = 1, lenght_km=0.1, r_ohm_per_km = .01, x_ohm_per_km = 0.05, c_nf_per_km = 10, max_i_ka = 0.4, name = “line1”)

Input Parameters

net.line

Parameter	Datatype	Value Range	Explanation
name	string		name of the line
std_type	string		standard type which can be used to easily define line parameters with the pandapower standard type library
from_bus*	integer		Index of bus where the line starts
to_bus*	integer		Index of bus where the line ends
length_km*	float	\(>\) 0	length of the line [km]
r_ohm_per_km*	float	\(\geq\) 0	resistance of the line [Ohm per km]
x_ohm_per_km*	float	\(\geq\) 0	reactance of the line [Ohm per km]
c_nf_per_km*	float	\(\geq\) 0	capacitance of the line (line-to-earth) [nano Farad per km]
r0_ohm_per_km****	float	\(\geq\) 0	zero sequence resistance of the line [Ohm per km]
x0_ohm_per_km****	float	\(\geq\) 0	zero sequence reactance of the line [Ohm per km]
c0_nf_per_km****	float	\(\geq\) 0	zero sequence capacitance of the line [nano Farad per km]
g_us_per_km*	float	\(\geq\) 0	dielectric conductance of the line [micro Siemens per km]
max_i_ka*	float	\(>\) 0	maximal thermal current [kilo Ampere]
parallel*	integer	\(\geq\) 1	number of parallel line systems
df*	float	0…1	derating factor (scaling) for max_i_ka
type	string	Naming conventions: “ol” - overhead line “cs” - underground cable system	type of line
max_loading_percent**	float	\(>\) 0	Maximum loading of the line
endtemp_degree***	float	\(>\) 0	Short-Circuit end temperature of the line
in_service*	boolean	True / False	specifies if the line is in service.

*necessary for executing a balanced power flow calculation
**optimal power flow parameter
***short-circuit calculation parameter
**** necessary for executing a three phase power flow / single phase short circuit .. note:

Defining a line with length zero leads to a division by zero in the power flow and is therefore not allowed. Lines with a very low impedance might lead to convergence problems in the power flow
for the same reason. If you want to directly connect two buses, please use the switch element instead of a line with a small impedance!

net.line_geodata

Parameter	Datatype	Explanation
coords	list	List of (x,y) tuples that mark the inflexion points of the line

Electric Model

Lines are modelled with the \(\pi\)-equivalent circuit:

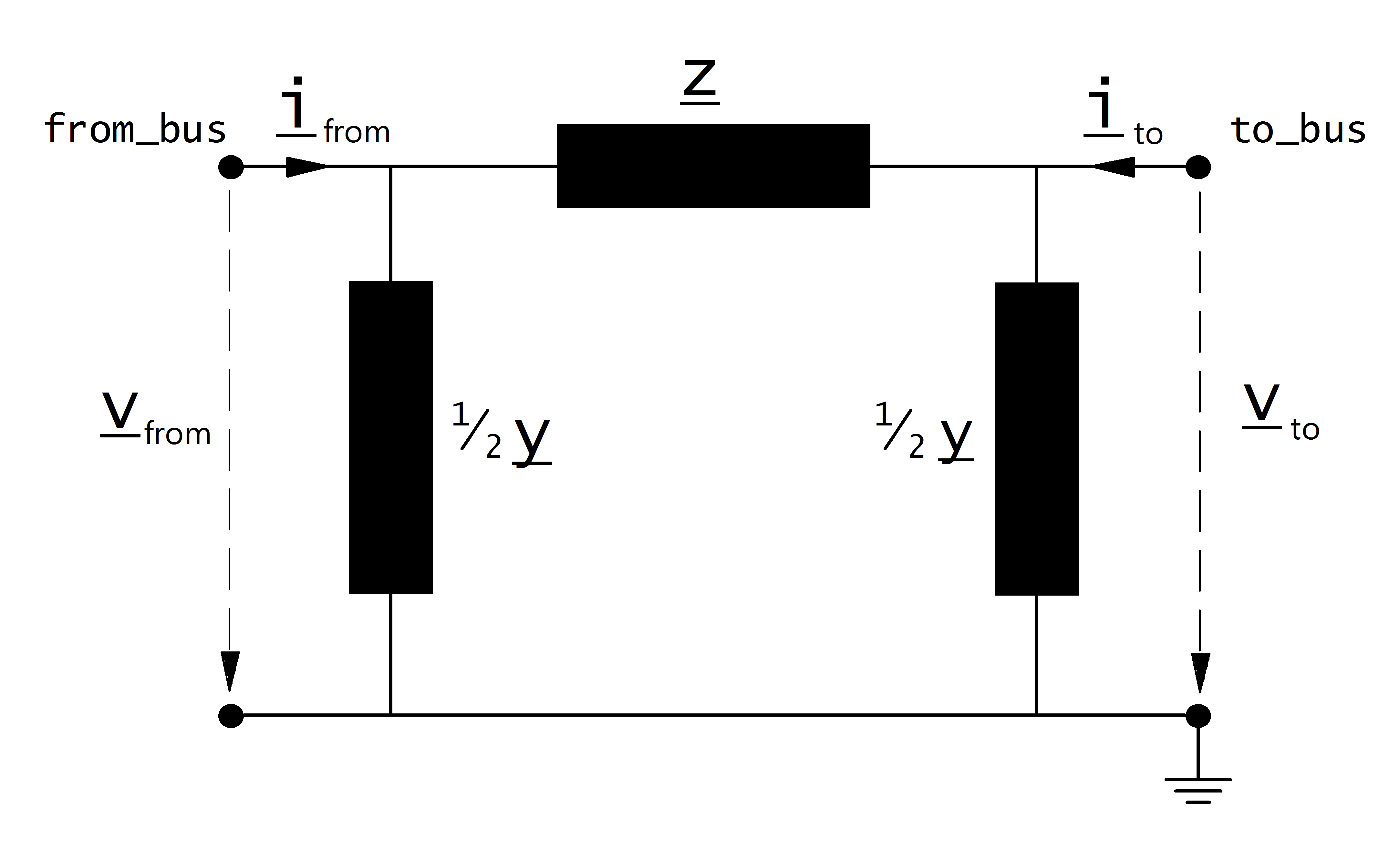
Three phase line model

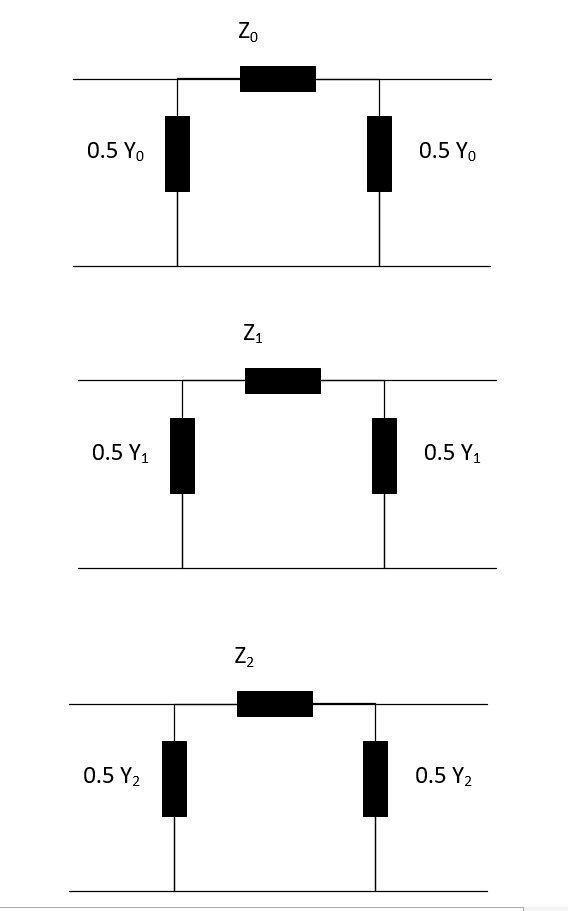
The elements in the equivalent circuit are calculated from the parameters in the net.line dataframe as:

\begin{align*} \underline{Z_{1 or 2}} &= (r\_ohm\_per\_km + j \cdot x\_ohm\_per\_km) \cdot \frac{length\_km}{parallel} \\ \underline{Y_{1 or 2}}&= (g\_us\_per\_km \cdot 1 \cdot 10^-6 + j \cdot 2 \pi f \cdot c\_nf\_per\_km \cdot 1 \cdot 10^-9) \cdot length\_km \cdot parallel\\ \underline{Z_{0}} &= (r0\_ohm\_per\_km + j \cdot x0\_ohm\_per\_km) \cdot \frac{length\_km}{parallel} \\ \underline{Y_{0}} &= (g\_us\_per\_km \cdot 1 \cdot 10^-6 + j \cdot 2 \pi f \cdot c0\_nf\_per\_km \cdot 1 \cdot 10^-9) \cdot length\_km \cdot parallel \end{align*}

The power system frequency \(f\) is defined when creating an empty network, the default value is \(f = 50 Hz\).

Note

For three phase load flow, three decoupled sequence networks ( zero , positive and negtive) are considered.

Positive and Negative sequence impedances are given by r_ohm_per_km, x_ohm_per_km, and c_nf_per_km

Zero sequence impedances are given by r0_ohm_per_km, x0_ohm_per_km, and c0_nf_per_km

The parameters are then transformed in the per unit system:

\begin{align*} Z_{N} &= \frac{V_{N}^2}{S_{N}} \\ \underline{z} &= \frac{\underline{Z}}{Z_{N}} \\ \underline{y} &= \underline{Y} \cdot Z_{N} \\ \end{align*}

Where the reference voltage \(V_{N}\) is the nominal voltage at the from bus and the rated apparent power \(S_{N}\) is defined system wide in the net object (see Unit Systems and Conventions).

Note

pandapower assumes that nominal voltage of from bus and to bus are equal, which means pandapower does not support lines that connect different voltage levels. If you want to connect different voltage levels, either use a transformer or an impedance element.

Result Parameters

net.res_line

Parameter	Datatype	Explanation
p_from_mw	float	active power flow into the line at “from” bus [MW]
q_from_mvar	float	reactive power flow into the line at “from” bus [MVar]
p_to_mw	float	active power flow into the line at “to” bus [MW]
q_to_mvar	float	reactive power flow into the line at “to” bus [MVar]
pl_mw	float	active power losses of the line [MW]
ql_mvar	float	reactive power consumption of the line [MVar]
i_from_ka	float	Current at from bus [kA]
i_to_ka	float	Current at to bus [kA]
i_ka	float	Maximum of i_from_ka and i_to_ka [kA]
vm_from_pu	float	voltage magnitude at from bus
vm_to_pu	float	voltage magnitude at to bus
va_from_degree	float	voltage angle at from bus [degrees]
va_to_degree	float	voltage angle at to bus [degrees]
loading_percent	float	line loading [%]

The power flow results in the net.res_line table are defined as:

\begin{align*} p\_from\_mw &= Re(\underline{v}_{from} \cdot \underline{i}^*_{from}) \\ q\_from\_mvar &= Im(\underline{v}_{from} \cdot \underline{i}^*_{from}) \\ p\_to\_mw &= Re(\underline{v}_{to} \cdot \underline{i}^*_{to}) \\ q\_to\_mvar &= Im(\underline{v}_{to} \cdot \underline{i}^*_{to}) \\ pl\_mw &= p\_from\_mw + p\_to\_mw \\ ql\_mvar &= q\_from\_mvar + q\_to\_mvar \\ i\_from\_ka &= i_{from} \\ i\_to\_ka &= i_{to} \\ i\_ka &= max(i_{from}, i_{to}) \\ loading\_percent &= \frac{i\_ka}{imax\_ka \cdot df \cdot parallel} \cdot 100 \end{align*}

net.res_line_3ph

Parameter	Datatype	Explanation
p_a_from_mw	float	active power flow into the line at from bus: Phase A [MW]
q_a_from_mvar	float	reactive power flow into the line at from bus : Phase A[MVar]
p_b_from_mw	float	active power flow into the line at from bus: Phase B [MW]
q_b_from_mvar	float	reactive power flow into the line at from bus : Phase B[MVar]
p_c_from_mw	float	active power flow into the line at from bus: Phase C [MW]
q_c_from_mvar	float	reactive power flow into the line at from bus : Phase C[MVar]
p_a_to_mw	float	active power flow into the line at to bus: Phase A [MW]
q_a_to_mvar	float	reactive power flow into the line at to bus : Phase A[MVar]
p_b_to_mw	float	active power flow into the line at to bus: Phase B [MW]
q_b_to_mvar	float	reactive power flow into the line at to bus : Phase B[MVar]
p_c_to_mw	float	active power flow into the line at to bus: Phase C [MW]
q_c_to_mvar	float	reactive power flow into the line at to bus : Phase C[MVar]
pl_a_mw	float	active power losses of the line: Phase A [MW]
ql_a_mvar	float	reactive power consumption of the line: Phase A [MVar]
pl_b_mw	float	active power losses of the line: Phase B [MW]
ql_b_mvar	float	reactive power consumption of the line: Phase B [MVar]
pl_c_mw	float	active power losses of the line: Phase C [MW]
ql_c_mvar	float	reactive power consumption of the line: Phase C [MVar]
i_a_from_ka	float	Current at from bus: Phase A [kA]
i_b_from_ka	float	Current at from bus: Phase B [kA]
i_c_from_ka	float	Current at from bus: Phase C [kA]
i_n_from_ka	float	Current at from bus: Neutral [kA]
i_a_to_ka	float	Current at to bus: Phase A [kA]
i_b_to_ka	float	Current at to bus: Phase B [kA]
i_c_to_ka	float	Current at to bus: Phase C [kA]
i_n_to_ka	float	Current at to bus: Neutral [kA]
i_ka	float	Maximum of i_from_ka and i_to_ka [kA]
loading_percent	float	line loading [%]

The power flow results in the net.res_line_3ph table are defined as:

\begin{align*} p\_from\_mw_{phase} &= Re(\underline{v_{phase}}_{from} \cdot \underline{i_{phase}}^*_{from}) \\ q\_from\_mvar_{phase} &= Im(\underline{v_{phase}}_{from} \cdot \underline{i_{phase}}^*_{from}) \\ p\_to\_mw_{phase} &= Re(\underline{v_{phase}}_{to} \cdot \underline{i_{phase}}^*_{to}) \\ q\_to\_mvar_{phase} &= Im(\underline{v_{phase}}_{to} \cdot \underline{i_{phase}}^*_{to}) \\ pl\_mw_{phase} &= p\_from\_mw_{phase} + p\_to\_mw_{phase} \\ ql\_mvar_{phase} &= q\_from\_mvar_{phase} + q\_to\_mvar_{phase} \\ i\_from\_ka_{phase} &= i_{from_{phase}} \\ i\_to\_ka_{phase} &= i_{to_{phase}} \\ i\_ka &= max(i_{from}, i_{to}) \\ i\_from\_ka_{neutral} &= |i_{from_{phaseA}}| + |i_{from_{phaseB}}| + |i_{from_{phaseC}}|\\ i\_to\_ka_{neutral} &= |i_{to_{phaseA}}| + |i_{to_{phaseB}}| + |i_{to_{phaseC}}| \\ loading\_percent &= \frac{i\_ka}{imax\_ka \cdot df \cdot parallel} \cdot 100 \end{align*}

net.res_line_est

The state estimation results are put into net.res_line_est with the same definition as in net.res_line.

Parameter	Datatype	Explanation
p_from_mw	float	active power flow into the line at “from” bus [MW]
q_from_mvar	float	reactive power flow into the line at “from” bus [MVar]
p_to_mw	float	active power flow into the line at “to” bus [MW]
q_to_mvar	float	reactive power flow into the line at “to” bus [MVar]
pl_mw	float	active power losses of the line [MW]
ql_mvar	float	reactive power consumption of the line [MVar]
i_from_ka	float	Current at from bus [kA]
i_to_ka	float	Current at to bus [kA]
i_ka	float	Maximum of i_from_ka and i_to_ka [kA]
vm_from_pu	float	voltage magnitude at from bus
vm_to_pu	float	voltage magnitude at to bus
va_from_degree	float	voltage angle at from bus [degrees]
va_to_degree	float	voltage angle at to bus [degrees]
loading_percent	float	line loading [%]

net.res_line_sc

The short-circuit (SC) results are put into net.res_line_sc with following definitions:

Parameter	Datatype	Explanation
ikss_ka	float	initial short-circuit current value [kA]
ikss_from_ka	float	magnitude of the initial SC current at “”from”” bus [kA]
ikss_from_degree	float	degree of the initial SC current at “”from”” bus [degrees]
ikss_to_ka	float	magnitude of the initial SC current at “”to”” bus [kA]
ikss_to_degree	float	degree of the initial SC current at “”to”” bus [degrees]
p_from_mw	float	active SC power flow into the line at “”from”” bus [MW]
q_from_mvar	float	reactive SC power flow into the line at “”from”” bus [MVar]
p_to_mw	float	active SC power flow into the line at “”to”” bus [MW]
q_to_mvar	float	reactive SC power flow into the line at “”to”” bus [MVar]
vm_from_pu	float	voltage magnitude at “”from”” bus [p.u.]
vm_to_pu	float	voltage magnitude at “”to”” bus [p.u.]
va_from_degree	float	voltage angle at “”from”” bus [degrees]
va_to_degree	float	voltage angle at “”to”” bus [degrees]
ip_ka	float	peak value of the short-circuit current [kA]
ith_ka	float	equivalent thermal short-circuit current [kA]