Optimal Power Flow¶
Pandapower provides an interface for AC and DC optimal power flow calculations. In the following, it is presented how the optimisation problem can be formulated with the pandapower data format.
Note
We highly recommend the tutorials for the usage of the optimal power flow.
Optimisation problem¶
The equation describes the basic formulation of the optimal power flow problem. The pandapower optimal power flow can be constrained by either, AC and DC loadflow equations. The branch constraints represent the maximum apparent power loading of transformers and the maximum line current loadings. The bus constraints can contain maximum and minimum voltage magnitude and angle. For the external grid, generators, loads, DC lines and static generators, the maximum and minimum active resp. reactive power can be considered as operational constraints for the optimal power flow. The constraints are defined element wise in the respective element tables.
Generator Flexibilities / Operational power constraints
The active and reactive power generation of generators, loads, dc lines and static generators can be defined as a flexibility for the OPF.
| Constraint | Defined in |
| \(P_{min,i} \leq P_{g} \leq P_{max,g}, g \ \epsilon \ gen\) | net.gen.min_p_kw / net.gen.max_p_kw |
| \(Q_{min,g} \leq Q_{g} \leq Q_{max,g}, g \ \epsilon \ gen\) | net.gen.min_q_kvar / net.gen.max_q_kvar |
| \(P_{min,sg} \leq P_{sg} \leq P_{max,sg}, sg \ \epsilon \ sgen\) | net.sgen.min_p_kw / net.sgen.max_p_kw |
| \(Q_{min,sg} \leq Q_{sg} \leq Q_{max,sg}, sg \ \epsilon \ sgen\) | net.sgen.min_q_kvar / net.sgen.max_q_kvar |
| \(P_{max,g}, g \ \epsilon \ dcline\) | net.dcline.max_p_kw |
| \(Q_{min,g} \leq Q_{g} \leq Q_{max,g}, g \ \epsilon \ dcline\) | net.dcline.min_q_from_kvar / net.dcline.max_q_from_kvar / net.dcline.min_q_to_kvar / net.dcline.max_q_to_kvar |
| \(P_{min,eg} \leq P_{eg} \leq P_{max,eg}, eg \ \epsilon \ ext_grid\) | net.ext_grid.min_p_kw / net.ext_grid.max_p_kw |
| \(Q_{min,eg} \leq Q_{eg} \leq Q_{max,eg}, eg \ \epsilon \ ext_grid\) | net.ext_grid.min_q_kvar / net.ext_grid.max_q_kvar |
| \(P_{min,ld} \leq P_{ld} \leq P_{max,ld}, ld \ \epsilon \ load\) | net.sgen.min_p_kw / net.sgen.max_p_kw |
| \(Q_{min,ld} \leq Q_{ld} \leq Q_{max,ld}, ld \ \epsilon \ load\) | net.sgen.min_q_kvar / net.sgen.max_q_kvar |
Note
Defining operational constraints is indispensable for the OPF, it will not start if contraints are not defined.
Network Constraints
The network constraints contain constraints for bus voltages and branch flows:
| Constraint | Defined in |
| \(V_{min,j} \leq V_{g,i} \leq V_{min,i}, j \ \epsilon \ bus\) | net.bus.min_vm_pu / net.bus.max_vm_pu |
| \(L_{k} \leq L_{max,k}, k \ \epsilon \ trafo\) | net.trafo.max_loading_percent |
| \(L_{l} \leq L_{max,l}, l \ \epsilon \ line\) | net.line.max_loading_percent |
| \(L_{l} \leq L_{max,l}, l \ \epsilon \ trafo_{3w}\) | net.trafo3w.max_loading_percent |
The defaults are 100% loading for branch elements and +-0.1 p.u. for bus voltages.
Cost functions¶
The cost function is specified element wise and is organized in tables as well, which makes the parametrization user friendly. There are two options formulating a cost function for each element: A piecewise linear function with $n$ data points.
Piecewise linear cost functions can be specified using create_piecewise_linear_costs():
-
pandapower.create_piecewise_linear_cost(net, element, element_type, data_points, type='p', index=None)¶ - Creates an entry for piecewise linear costs for an element. The currently supported elements are
- Generator
- External Grid
- Static Generator
- Load
- Dcline
- Storage
- INPUT:
element (int) - ID of the element in the respective element table
element_type (string) - Type of element [“gen”, “sgen”, “ext_grid”, “load”, “dcline”, “storage”] are possible
data_points - (numpy array) Numpy array containing n data points (see example)
- OPTIONAL:
type - (string) - Type of cost [“p”, “q”] are allowed
index (int, index) - Force a specified ID if it is available. If None, the index one higher than the highest already existing index is selected.
- OUTPUT:
- index (int) - The unique ID of created cost entry
- EXAMPLE:
- create_piecewise_linear_cost(net, 0, “load”, np.array([[0, 0], [75, 50], [150, 100]]))
- NOTE:
- costs for reactive power can only be quadratic, linear or constant. No higher grades supported.
- costs for storages are positive per definition (similar to sgen costs)
The other option is to formulate a n-polynomial cost function:
Polynomial cost functions can be speciefied using create_polynomial_cost():
-
pandapower.create_polynomial_cost(net, element, element_type, coefficients, type='p', index=None)¶ - Creates an entry for polynomial costs for an element. The currently supported elements are
- Generator
- External Grid
- Static Generator
- Load
- Dcline
- Storage
- INPUT:
element (int) - ID of the element in the respective element table
element_type (string) - Type of element [“gen”, “sgen”, “ext_grid”, “load”, “dcline”, “storage”] are possible
data_points - (numpy array) Numpy array containing n cost coefficients, starting with highest order (see example)
**type ** -“p” or “q”
- OPTIONAL:
type - (string) - Type of cost [“p”, “q”] are allowed
index (int, None) - Force a specified ID if it is available. If None, the index one higher than the highest already existing index is selected.
- OUTPUT:
- index (int) - The unique ID of created cost entry
- EXAMPLE:
- create_polynomial_cost(net, 0, “gen”, np.array([0, 1, 0]))
- NOTE:
- costs for storages are positive per definition (similar to sgen costs)
Note
Please note, that polynomial costs for reactive power can only be quadratic, linear or constant. Piecewise linear cost funcions for reactive power are not working at the moment with 2 segments or more. Loads can only have 2 data points in their piecewise linear cost function for active power.
Active and reactive power costs are calculted seperately. The costs of all types are summed up to determine the overall costs for a grid state.
Visualization of cost functions¶
Minimizing Generation
The most common optimization goal is the minimization of the overall generator feed in. The according cost function would be formulated like this:
pp.create_polynomial_cost(net, 0, 'sgen', np.array([-1, 0]))
pp.create_polynomial_cost(net, 0, 'gen', np.array([-1, 0]))
pp.create_polynomial_cost(net, 0, 'ext_grid', np.array([-1, 0]))
pp.create_piecewise_linear_cost(net, 0, "sgen", np.array([[net.sgen.min_p_kw.at[0], 1000], [0, 0]]))
pp.create_piecewise_linear_cost(net, 0, "gen", np.array([[net.gen.min_p_kw.at[0], 1000], [0, 0]]))
pp.create_piecewise_linear_cost(net, 0, "ext_grid", np.array([[-1e9, 1e9], [1e9, -1e9]]))
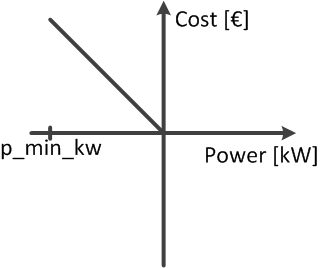
It is a straight with a negative slope, so that it has the highest cost value at p_min_kw and is zero when the feed in is zero:
Maximizing generation
This cost function may be used, when the curtailment of renewables should be minimized, which at the same time means that the feed in of those renewables should be maximized. This can be realized by the following cost function definitions:
pp.create_polynomial_cost(net, 0, 'sgen', np.array([1, 0]))
pp.create_polynomial_cost(net, 0, 'gen', np.array([1, 0]))
pp.create_piecewise_linear_cost(net, 0, "sgen", np.array([[net.sgen.min_p_kw.at[0], -1000], [0, 0]]))
pp.create_piecewise_linear_cost(net, 0, "gen", np.array([[net.gen.min_p_kw.at[0], -1000], [0, 0]]))
pp.create_piecewise_linear_cost(net, 0, "ext_grid", np.array([[-1e9, -1e9], [1e9, 1e9]]))
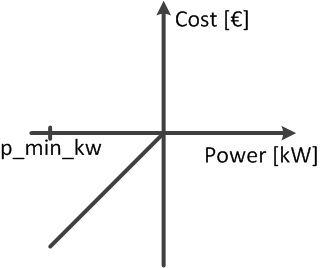
It is a straight with a positive slope, so that the cost is zero at p_min_kw and is at its maximum when the generation equals zero.
Maximize load
In case that the load should be maximized, the cost function could be defined like this:
pp.create_polynomial_cost(net, 0, 'load', np.array([-1, 0]))
pp.create_polynomial_cost(net, 0, 'storage', np.array([-1, 0]))
pp.create_piecewise_linear_cost(net, 0, "sgen", np.array([[0, 0], [net.load.max_p_kw.at[0], -1000]]))
pp.create_piecewise_linear_cost(net, 0, "gen", np.array([[net.storage.min_p_kw.at[0], 1000], [net.storage.max_p_kw.at[0], -1000]]))
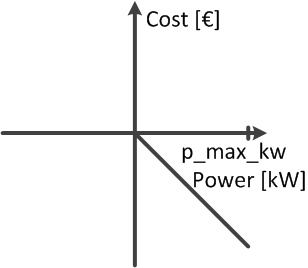
Minimizing load
In case that the load should be minimized, the cost function could be defined like this:
pp.create_polynomial_cost(net, 0, 'load', np.array([1, 0]))
pp.create_polynomial_cost(net, 0, 'storage', np.array([1, 0]))
pp.create_piecewise_linear_cost(net, 0, "sgen", np.array([[0, 0], [net.load.max_p_kw.at[0], 1000]]))
pp.create_piecewise_linear_cost(net, 0, "gen", np.array([[net.storage.min_p_kw.at[0], -1000], [net.storage.max_p_kw.at[0], 1000]]))
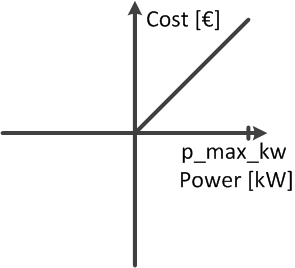
DC line behaviour
Please note, that the costs of the DC line transmission are always related to the power at the from_bus!
You can always check your Optimization result by comparing your result (From res_sgen, res_load etc.)
Parametrisation of the calculation¶
The internal solver uses the interior point method. By default, the initial state is the center of the operational constraints. Another option would be to initialize the optimisation with a valid loadflow solution. For optimiation of a timeseries, this warm start possibilty could imply a significant speedup. This is not yet provided in the actual version, but could be an useful extension in the future. Another parametrisation for the AC OPF is, if voltage angles should be considered, which is the same option than for the loadflow calculation with pandapower.runpp:
-
pandapower.runopp(net, verbose=False, calculate_voltage_angles=False, check_connectivity=False, suppress_warnings=True, r_switch=0.0, delta=1e-10, init='flat', numba=True, trafo3w_losses='hv', **kwargs)¶ Runs the pandapower Optimal Power Flow. Flexibilities, constraints and cost parameters are defined in the pandapower element tables.
Flexibilities can be defined in net.sgen / net.gen /net.load net.sgen.controllable if a static generator is controllable. If False, the active and reactive power are assigned as in a normal power flow. If True, the following flexibilities apply:
- net.sgen.min_p_kw / net.sgen.max_p_kw
- net.sgen.min_q_kvar / net.sgen.max_q_kvar
- net.load.min_p_kw / net.load.max_p_kw
- net.load.min_q_kvar / net.load.max_q_kvar
- net.gen.min_p_kw / net.gen.max_p_kw
- net.gen.min_q_kvar / net.gen.max_q_kvar
- net.ext_grid.min_p_kw / net.ext_grid.max_p_kw
- net.ext_grid.min_q_kvar / net.ext_grid.max_q_kvar
- net.dcline.min_q_to_kvar / net.dcline.max_q_to_kvar / net.dcline.min_q_from_kvar / net.dcline.max_q_from_kvar
Controllable loads behave just like controllable static generators. It must be stated if they are controllable. Otherwise, they are not respected as flexibilities. Dc lines are controllable per default
- Network constraints can be defined for buses, lines and transformers the elements in the following columns:
- net.bus.min_vm_pu / net.bus.max_vm_pu
- net.line.max_loading_percent
- net.trafo.max_loading_percent
- net.trafo3w.max_loading_percent
How these costs are combined into a cost function depends on the cost_function parameter.
- INPUT:
- net - The pandapower format network
- OPTIONAL:
verbose (bool, False) - If True, some basic information is printed
suppress_warnings (bool, True) - suppress warnings in pypower
If set to True, warnings are disabled during the loadflow. Because of the way data is processed in pypower, ComplexWarnings are raised during the loadflow. These warnings are suppressed by this option, however keep in mind all other pypower warnings are suppressed, too.init (str, “flat”) - init of starting opf vector. Options are “flat” or “pf”
Starting solution vector (x0) for opf calculations is determined by this flag. Options are: “flat” (default): starting vector is (upper bound - lower bound) / 2 “pf”: a power flow is executed prior to the opf and the pf solution is the starting vector. This may improve convergence, but takes a longer runtime (which are probably neglectible for opf calculations)
- References:
- “On the Computation and Application of Multi-period Security-Constrained Optimal Power Flow for Real-time Electricity Market Operations”, Cornell University, May 2007.
- H. Wang, C. E. Murillo-Sanchez, R. D. Zimmerman, R. J. Thomas, “On Computational Issues of Market-Based Optimal Power Flow”, IEEE Transactions on Power Systems, Vol. 22, No. 3, Aug. 2007, pp. 1185-1193.
- R. D. Zimmerman, C. E. Murillo-Sánchez, and R. J. Thomas, “MATPOWER: Steady-State Operations, Planning and Analysis Tools for Power Systems Research and Education,” Power Systems, IEEE Transactions on, vol. 26, no. 1, pp. 12-19, Feb. 2011.