Extended Ward¶
See also
Create Function¶
-
pandapower.create_xward(net, bus, ps_kw, qs_kvar, pz_kw, qz_kvar, r_ohm, x_ohm, vm_pu, in_service=True, name=None, index=None)¶ Creates an extended ward equivalent.
A ward equivalent is a combination of an impedance load, a PQ load and as voltage source with an internal impedance.
- INPUT:
net - The pandapower net within the impedance should be created
bus (int) - bus of the ward equivalent
ps_kw (float) - active power of the PQ load
qs_kvar (float) - reactive power of the PQ load
pz_kw (float) - active power of the impedance load in kW at 1.pu voltage
qz_kvar (float) - reactive power of the impedance load in kVar at 1.pu voltage
vm_pu (float)
- OUTPUT:
- xward id
Result Parameters¶
net.xward
| Parameter | Datatype | Value Range | Explanation |
| name | string | name of the extended ward equivalent | |
| bus* | integer | index of connected bus | |
| ps_kw* | float | constant active power demand [kW] | |
| qs_kvar* | float | constant reactive power demand [kVar] | |
| pz_kw* | float | constant impedance active power demand at 1.0 pu [kW] | |
| qz_kvar* | float | constant impedance reactive power demand at 1.0 pu [kVar] | |
| r_pu* | float | \(>\) 0 | internal resistance of the voltage source [p.u] |
| x_pu* | float | \(>\) 0 | internal reactance of the voltage source [p.u] |
| vm_pu* | float | \(>\) 0 | voltage source set point [p.u] |
| in_service* | boolean | True / False | specifies if the extended ward equivalent is in service. |
*necessary for executing a power flow calculation.
Electric Model¶
The extended ward equivalent is a ward equivalent: with additional PV-node with an internal resistance.
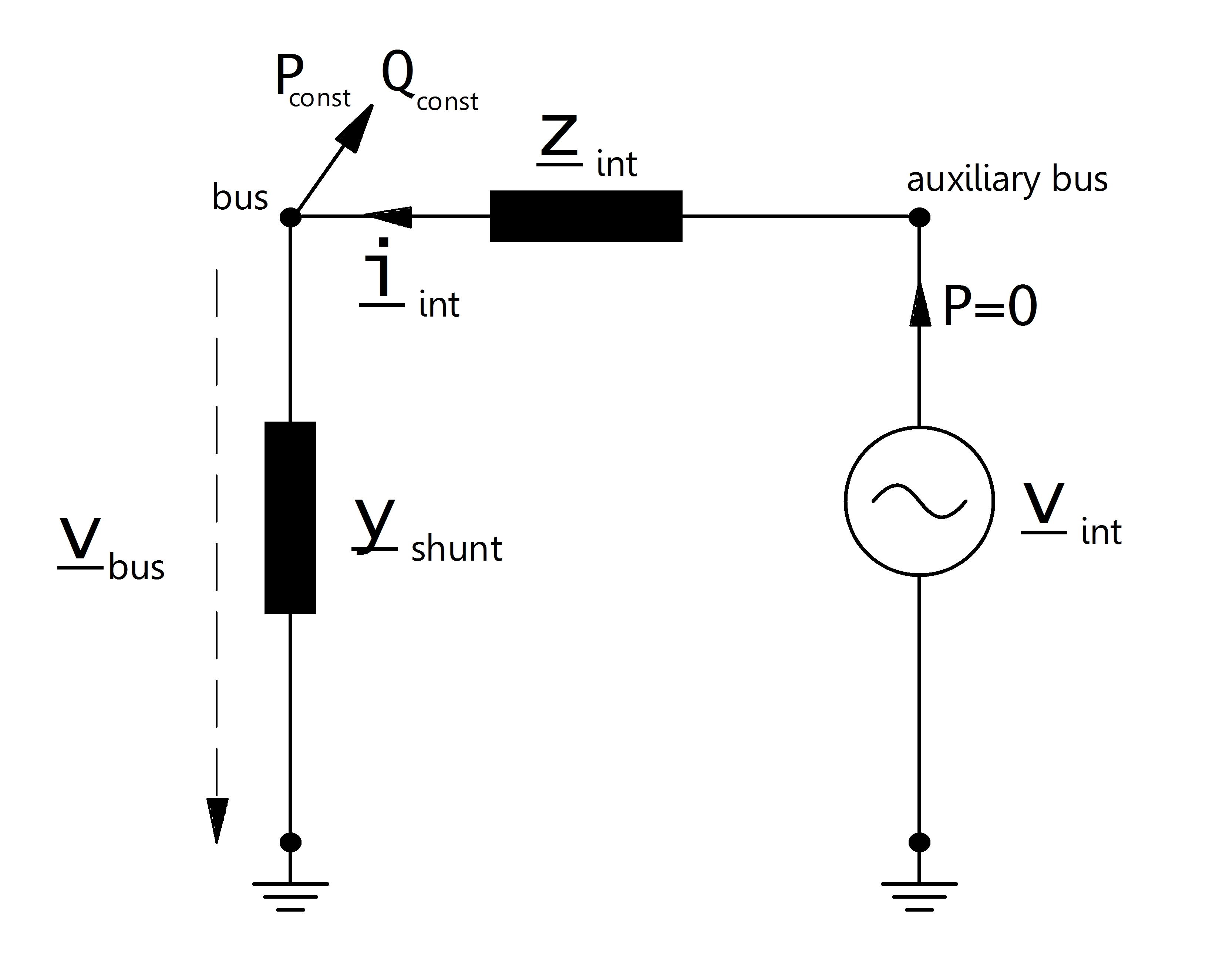
The constant apparent power is given by:
The shunt admittance part of the extended ward equivalent is calculated as described here:
The internal resistance is defined as:
The internal voltage source is modelled as a PV-node (generator) with:
Result Parameters¶
net.res_xward
| Parameter | Datatype | Explanation |
| p_kw | float | active power demand of the ward equivalent [kW] |
| q_kvar | float | reactive power demand of the ward equivalent [kVar] |
| vm_pu | float | voltage at the ward bus [p.u] |